论文阅读 "TetGen, a Delaunay-Based Quality Tetrahedral Mesh Generator"

METHOD OVERVIEW

The methodology of TetGen is a mixture of a classical boundary constrained methods [George et al. 1991] and a classical Delaunay refinement method [Ruppert 1995; Shewchuk 1998b]. This approach well combines engineering and theoretical ideas. It is efficient in generating a good quality tetrahedral mesh.

piecewise linear complex（PLC)

1. the boundary of each cell in $X$ is a union of cells in $X$ ;
2. if two distinct cells $F$, $G ∈ X$ intersect, their intersection is a union of cells in $X$ , all having lower dimension than at least one of $F$ or $G$

Pipeline

1. Delaunay Tetrahadealization(DT)
2. Constrained Mesh Generation(User Defined constraints)
3. Quality Mesh Generation

Delaunay Tetrahedralization

the Bowyer-Watson and the randomized flip algorithms

• efficient vertex insertion (Bowyer-Watson algorithm)
  first sorts the points through a spatial point sorting scheme. Inserting points based on this order, each point can be located efficiently (in nearly constant time)

Constrained Tetrahedral Mesh Generation

2D Flip $\rightarrow$ 3D additional vertices(Steiner points)

Optimal locations and the minimum number of Steiner points

Constrained Delaunay Tetrahedralization (CDT)

1. Shewchuk proved a useful condition that guarantees the existence of a CDT without adding Steiner points when all input edges are Delaunay $\rightarrow$ Non Steiner points adding
2. edge removal algorithm :A key operation in the recovery of constraints is to remove an edge from a tetrahedral mesh. $\rightarrow$ With optimal Steiner points adding

Quality Tetrahedral Mesh Generation

how to generate a good quality mesh that is best according to a set of given criteria.

Appropriate Number of Steiner points

Delaunay refinement $\rightarrow$ provides guarantees on mesh quality and mesh element size simultaneously.(Badly shaped tetrahedra & not terminate when there are sharp features)

• Some badly shaped tetrahedra may remain. They are all located (within a bounded distance) near sharp features.
• uses a mesh improvement phase to remove slivers and improve mesh quality.

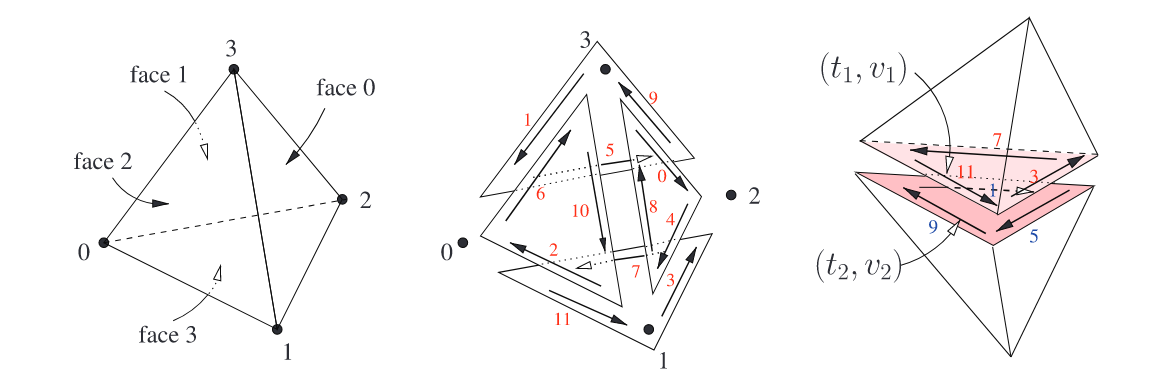
TETRAHEDRAL MESH DATA STRUCTURE

Basic

$\mathbf{T}$ :

• 4 pointer:each neighbor
• 4* 4-bit integer: each nerghbor
• 4 pointer:each vertice
• 16-bit integer: to setting flags,edges,ans tetrahadron itself

Primtive

handle: a pair $(t,v)$

• $t$ :a pointer to a tetrahedron
• $v$:an integer, called version

Moving Stratagy

1. Moving within the same edge ring：$(t, (v+i) mod 12)$，where $i ∈ {4, 8}$
2. Moving between two edge rings:a global lookup table$L[0 · · · 11]$
3. When traveling from one tetrahedron to one of its adjacent tetrahedra
   $(t_1.v_1)$ to $(t_2,v_2)$
   $t_2$ : logged inside $t_1$
   $v_2$: get from table

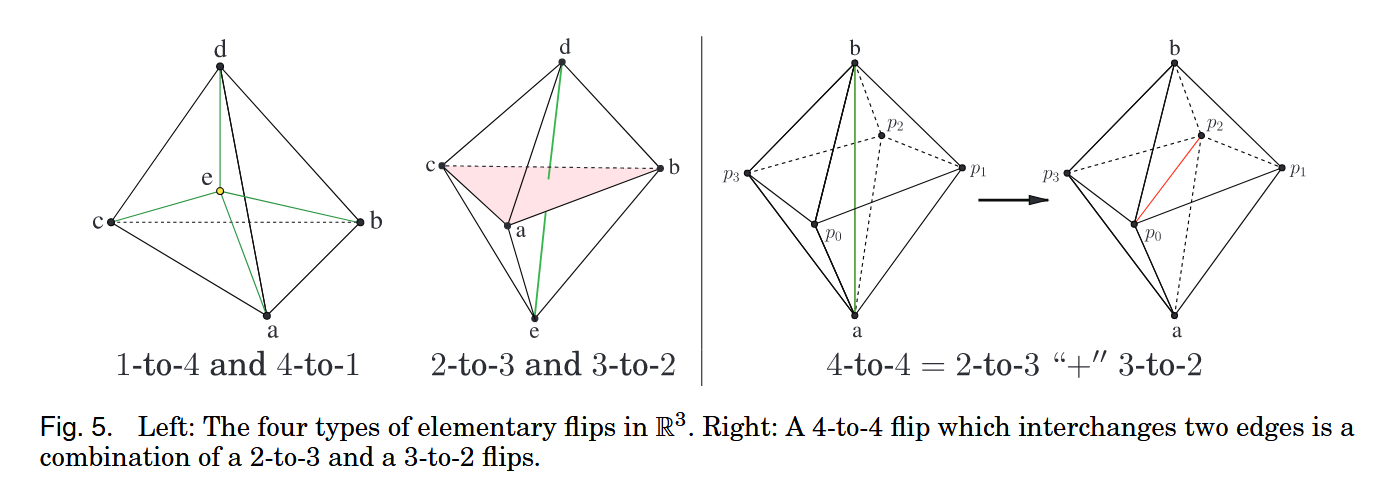
LOCAL MESH TRANSFORMATIONS

Elementary Flips

1-to-4

Insert/Deleting a vertex

2-to-3

inserting and deleting an edge

4-to-4（combination)

2-to-3 + 3-to-2

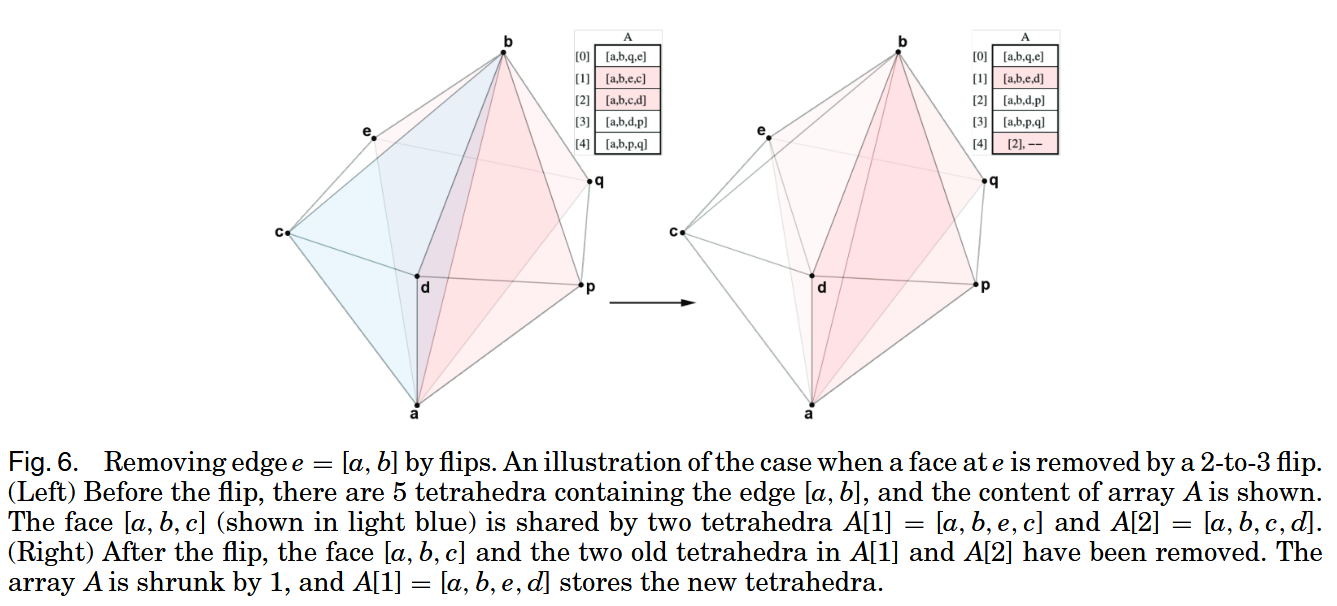
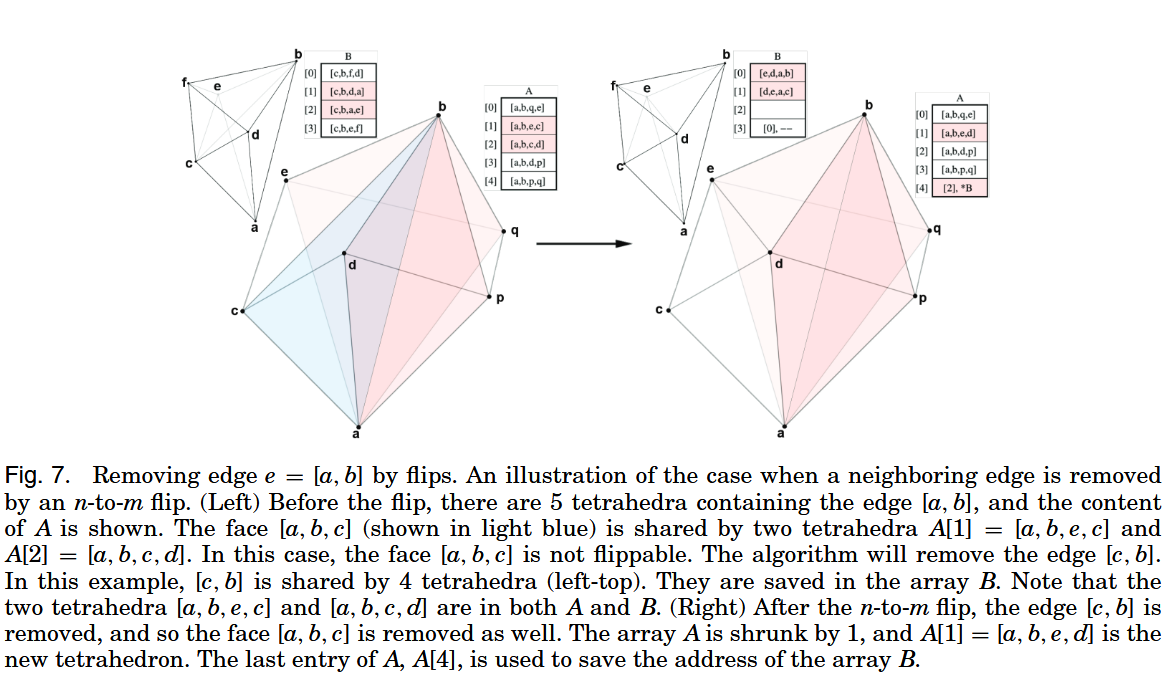
Edge Removal

reduce the cardinality$|A|$ of A by performing 2-to-3 flips(fig 6) to remove faces at the edge $e$，until either $|A| = 3$ or $|A| > 3$ - if $|A| = 3$,returns - if $|A| > 3$,tries to remove an edge e1 that contains one of the endpoints of e by an n-to-m flip(fig 7)

STEP

1. flipnm takes the array $A$ (whose size is n) as input,reduce the cardinality of $A$,returns the final cardinality $m$ of $A$,$m = 2$ ,means $e$ is removed
2. flipnm post,releases the memory allocated inside flipnm

Summary

1. If $n = 3$, then either e is removed by a flip32, or it is not flippable. It returns the current size m of A. Otherwise, it goes to step (2)
2. $(n > 3)$. It tries to remove a face in $F$ by flip23. If a face in $F$ is successfully flipped, then $|A|$ is reduced by 1 (Figure 6, Right). It then (recursively) calls $flipnm(A[0 · · · n − 2])$. When no face in $F$ can be removed, it goes to Step (3)
3. $(n > 3)$. It tries to remove an edge in $E$ by a flipnm. Let $e_1 ∈ E$ be such an edge. It first initializes an array $B[0 · · · n1 − 1]$ of $n_1$ tetrahedra sharing at $e_1$, where $n1 ≥ 3$, then it calls $m1 := flipnm(B[0 · · · n1 − 1])$. If e1 has been removed, then $|A|$ is reduced by 1 (Figure 7, Right). The last entry, $A[n − 1]$, is re-used to store the address of the array $B$ (so that the memory it occupies can be released later). It then (recursively) calls $flipnm( A[0 · · · n − 2])$. Otherwise, $e_1$ is not removed, it calls $flipnm_post(B[0 · · · n1 − 1], m1)$ to free the memory. If no edge in $E$ can be removed, it returns $|A|$

Vertex Insertion

Delaunay init

A vertex insertion can be implemented as a combination of elementary flips

• interior of a tetrahedron: 1-to-4
• on a shared face: combining 1-to-4 and 2-to-3
• on a shared edge & $n \ge 3$ :1-to-4 and $(n-2)$ 2-to-3
  Unified

1. deleting all tetrahedra that intersect the new vertex $v$,generating a polyhedron $C$
2. fill the polyhedron $C$ by its faces and vertex $v$
   Bowyer-Watson algorithm
   this cavity $C$ of $v$ can be enlarged such that it includes all tetrahedra in $T$ whose circumspheres contain $v$

Vertex insertion in a nonDelaunay tetrahedralization or a constraint tetrahedral mesh

Simplest way:to remove tetrahedra in the set $C$ incrementally until the reduced cavity $C$ becomes star-shaped
Robust: apply a sequence of flips to update the tetrahedralization

FILTERED EXACT GEOMETRIC PREDICATES

• orient3D test：decides the position of a point relative to a plane defined by three other noncollinear points
• in sphere test：decides whether a point lies in the relative inside or outside of a sphere defined by four other noncoplanar points.
  $orient3D(a, b, c, d) = sign(det(A))$ and $in _ sphere(a, b, c, d, e) = sign(det(B))$
  $$
  A = \begin{bmatrix}
  a_x & a_y & a_z & 1 \newline
  b_x & b_y & b_z & 1 \newline
  c_x & c_y & c_z & 1 \newline
  d_x & d_y & d_z & 1 \newline
  \end{bmatrix}
  $$
  $$
  B = \begin{bmatrix}
  a_x & a_y & a_z, & a_x^2 + a_y^2 + a_z^2 & 1 \newline
  b_x & b_y & b_z, & b_x^2 + b_y^2 + b_z^2 & 1 \newline
  c_x & c_y & c_z, & c_x^2 + c_y^2 + c_z^2 & 1 \newline
  d_x & d_y & d_z, & d_x^2 + d_y^2 + d_z^2 & 1 \newline
  e_x & e_y & e_z, & e_x^2 + e_y^2 + e_z^2 & 1 \newline
  \end{bmatrix}
  $$

Filtered Exact Predicates

arithmetic filters: evaluate in float first, estimate error,fall back to exact arithmetic if the error is too big to determine the sign

• static filters:previously computed,quickly answer many “easy cases”
• dynamic filters:within the program, are more accurate, but require more computational time

DELAUNAY TETRAHEDRALIZATIONS

Delaunay triangulation:a set of d-dimensional point set $V$ is a d-dimensional simplicial complex $D$ such that every simplex in $D$ has the empty sphere property
Any simplex whose vertices are in $V$ and it satisfies the empty sphere property is called a Delaunay simplex.

Incremental Construction

Point Location:Bowyer-Watson algorithm & incremental flip algorithm

Inserting one point at a time. Each point is first located, then inserted.

Boosting:
starting from a tetrahedron containing the last inserted point, the next point can be quickly located

• presorts the points,then inserts the points in this order.
• point location:stochastic walk algorithm:stochastic walk algorithm
• degenerate cases:used a simplified symbolic perturbation scheme ,that is, 5 or more points share a common sphere, so that the in $sphere _ test$ never returns a zero, thus there is always one canonical Delaunay tetrahedralization of any point set.

CONSTRAINED TETRAHEDRAL MESH GENERATION

2D:A triangulation T which contains a set L of noncrossing line segments can always be constructed by a modifiededge flip algorithm
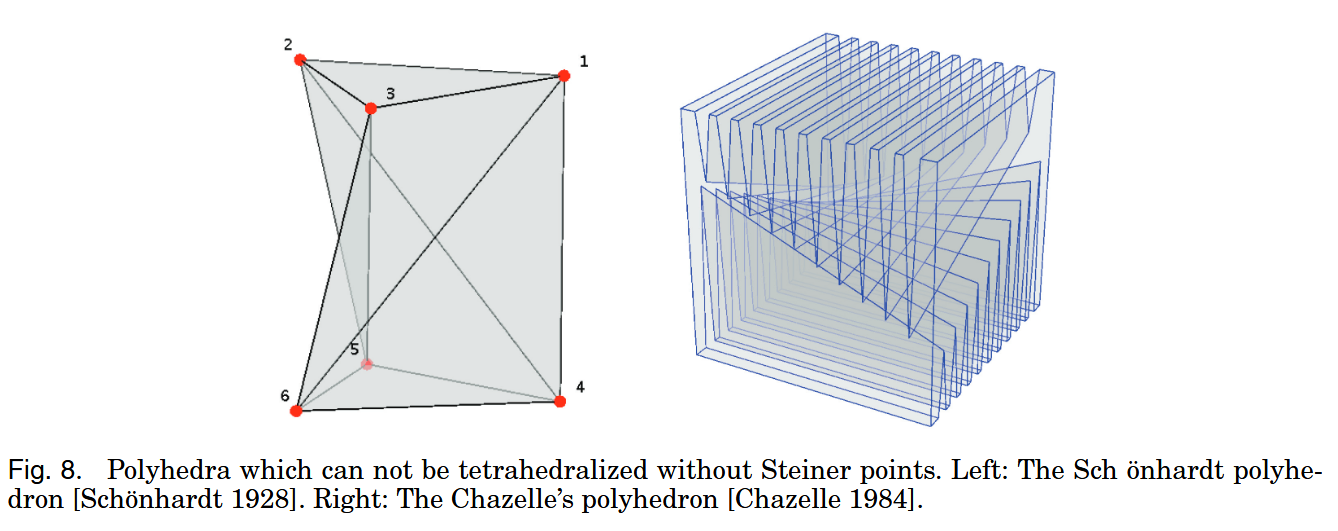
3D:There exist (nonconvex) polyhedra which have no tetrahedralization with its own vertices(Fig 8)

Subdividing Constraints

TetGen constructs a constrained Delaunay tetrahedralization (CDT)
CDTs have many nice properties similar to those of Delaunay tetrahedralizations Shewchuk 2008

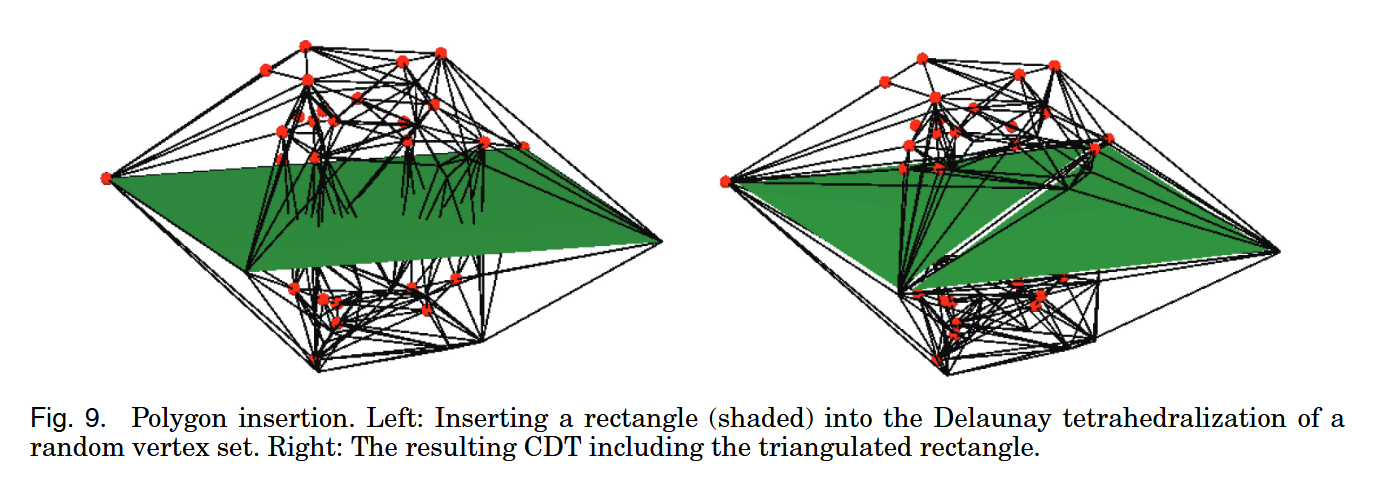
A crucial difference between a CDT and a (conforming) Delaunay tetrahedralization is that some triangles are not required to be Delaunay, which frees the CDT to better respect the constraints, refer to Figure 9 for an example.

Constrained Delaunay Tetrahedralizations

A triangle s in a tetrahedralization is said to be locally Delaunay if:

• it only belongs to one tetrahedra in $T$ or it is a face of two tetrahedra $t_1$ and $t_2$
• it has a circumscribed sphere that encloses no vertex of $t_1$ and $t_2$
  A tetrahedralization $T$ of a 3D PLC $X$ is a constrained Delaunay tetrahedralization (CDT) of $X$ if every triangle in $T$ not included in a polygon in $X$ is locally Delaunay.

Shewchuk’s condition:
A segment $e ∈ X$ is strongly Delaunay:A segment $e ∈ X$ is strongly Delaunay.

• If every segment of X is strongly Delaunay, then it has a CDT with no Steiner point.
• If a PLC $X$ does not satisfy this condition, it can always be transformed into another PLC $Y$ by adding a number of Steiner points on the segments of $X$ , such that $Y$ does have a CDT.It is called a Steiner CDT of $X$
  A (Steiner) CDT of a PLC $X$ is generated in three steps:

1. create the Delaunay tetrahedralization of the vertices of $X$
2. insert the segments of $X$
3. insert the polygons of $X$

Preserving Constraints

1. recover edges
2. recover triangles
3. vertex suppression(was described in George et al. )
   constraints are recovered by combining flips and Steiner points insertions & all those Steiner points added in constraints are either deleted or repositioned into the interior of the mesh.

Edge Recovery & Triangles Recovery

initializes an array of all edges to be recovered, then it recovers them one by one.

1. $f ∈ F_e$,2-to-3 flip if $f$ is flippable.
2. If not flippable, find an edge $e’$ causes $f$ not flippable,then remove $e’$
3. If $|F_e| = 1$ , it is “locked” and never be flipped
4. If $e$ cannot be recovered,split $e$ by adding s Steriner point in it(midpoint)

Recursive:flipnm operation will automatically search those flippable edges surrounding e and flip them
“level” parameter ($> 0$):limits the number of recursions inside a flipnm call

QUALITY TETRAHEDRAL MESH GENERATION

Tetrahedron Shape Measures

regular tetrahedron (whose edge lengths are all equal) is ideal.

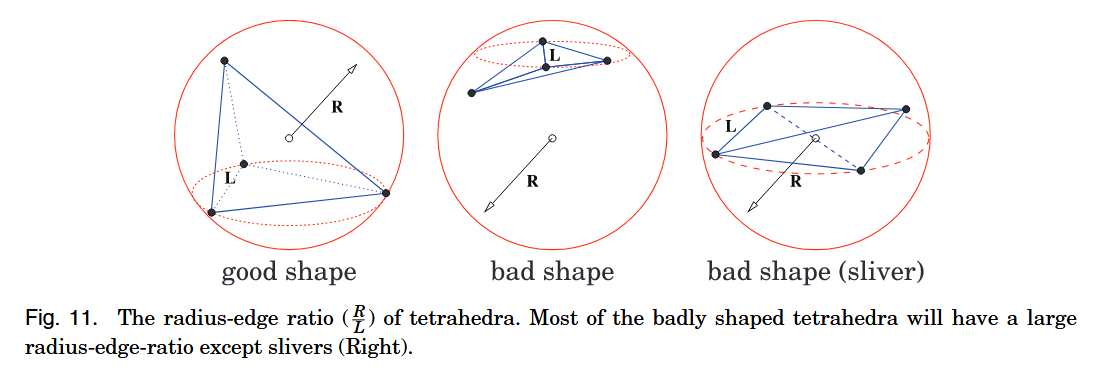
• aspect ratio $\eta(\tau)$:as the ratio between the longest edge length $l_{max}$ and the shortest height $h_{min}$ that is $\eta = \frac{l_{max}}{h_{min}}$
• radius-edge ratio$\rho(\tau)$:the ratio between the radius $R$ of its circumscribed ball and the length $L$ of its shortest edge,that is $\rho(\tau) = \frac{R}{L}\ge \frac{1}{2\sin \theta_{min}}$,where $\theta_{min}$ is the smallest face angle of $\tau$

Most of the badly shaped tetrahedra will have a big radius-edge ratio. However, a sliver can have a relatively small radius-edge ratio

Tetrahedral Mesh Refinement

mesh refinement problem:given a 3D PLC $X$ and an initial tetrahedral mesh of $T$ of $X$ , a set of tetrahedron shape measures, how to generate a tetrahedral mesh of $X$ with good-shaped tetrahedra.

how to place Steiner points efficiently so that a tetrahedral mesh containing these points simultaneously satisfies the desired properties
Delaunay refinement:it updates a conforming Delaunay mesh by inserting the circumcenters of bad-quality triangles or tetrahedra.(may produce slivers)

main limitation of Delaunay refinement is that it may not terminate if the input contains sharp features.TetGen uses a new mesh refinement algorithm.The boundary conformity and Steiner points insertion are well combined during the mesh refinement. Sharp features are recovered and maintained simultaneously by the CDT. This algorithm generates a tetrahedral mesh of the domain with well-shaped tetrahedra.

Constrained Delaunay Refinement

a positive constant $B$ that specifies the maximum permitted radius-edge ratio for tetrahedra
skinny if its radius-edge ratio exceeds $B$

a skinny tetrahedron can exist only if it adjoins (has at least one vertex lying on) the relative interior of a segment or polygon that forms a small angle. Every other tetrahedron is guaranteed not to be skinny.

refinement algorithm：skinny tetrahedra are “split” by new vertices inserted at their circumcenters, and “encroached” subsegments and subpolygons are split likewise. (a flip stratagy can be applied later)

However, the rules are modified so that small domain angles do not cause havoc.

$r_v$(insertion radius):the distance to the closest distinct vertex visible from $v$ at the moment when $v$ is first inserted into the PLC $Y$.

Problem:This breaks an endless cycle wherein ever-shorter edges drive the creation of yet shorter edges.

$rr_v$(relaxed insertion radius): most vertices, including all input vertices, $rr_v = r_v$,when the algorithm is forced to create a new edge that it considers to be unreasonably short, the newly inserted vertex $v$ has $rr_v$ greater than the length of that edge.($rr_v ≥ r_v$)

Mesh Improvement

• the possible existence of slivers
• in the adaptive mesh generation, some badly shaped tetrahedra may not be removed due to the mesh sizing limitation
  
  TetGen only focuses on the removal of tetrahedra which have the worst quality.

1. topological transformation, that is, face/edge flips and vertex insertion/deletion
2. vertex smoothing, that is, relocating vertices without changing the mesh topology

“hill climbing” scheme：a local operation is only performed if the resulting tetrahedra all have better quality than the worst quality of current tetrahedra.–